Deconstructing Disinformation on Student Growth Percentiles & Teacher Evaluation in New Jersey

Deconstructing Disinformation on Student Growth Percentiles & Teacher Evaluation in New Jersey (Printable Policy Brief): SGP_Disinformation_BakerOluwole

Bruce D. Baker, Rutgers University, Graduate School of Education

Joseph Oluwole, Montclair State University

Introduction

This brief addresses problems with, and disinformation about New Jersey’s Student Growth Percentile (SGP) measures which are proposed by New Jersey Department of Education officials, to be used for evaluating teachers and principals and rating local public schools. Specifically, the New Jersey Department of Education has proposed that the student growth percentile measures be used as a major component for determining teacher effectiveness:

“If, according to N.J.A.C. 6A:10-4.2(b), a teacher receives a median student growth percentile, the student achievement component shall be at least 35 percent and no more than 50 percent of a teacher’s evaluation rubric rating.” [1]

Yet those ratings of teacher effectiveness may have consequences for employment. Specifically, under proposed regulations, school principals are obligated to notify teachers:

“…in danger of receiving two consecutive years of ineffective or partially effective ratings, which may trigger tenure charges to be brought pursuant to TEACHNJ and N.J.A.C. 6A:3.”[2]

In addition, proposed regulations require that school principals and assistant principals be evaluated based on school aggregate growth percentile data:

“If, according to N.J.A.C. 6A:10-5.2(b), the principal, vice-principal, or assistant principal receives a median student growth percentile measure as described in N.J.A.C. 6A:10-5.2(c) below, the measure shall be at least 20 percent and no greater than 40 percent of evaluation rubric rating as determined by the Department.” [3]

Thus inferring that the median student’s achievement growth in any school may be causally attributed to the principal and/or vice principal.

But, we explain in this brief that student growth percentile data are not up to this task.  In the following brief, we explain that:

• Student Growth Percentiles are not designed for inferring teacher influence on student outcomes.
• Student Growth Percentiles do not control for various factors outside of the teacher’s control.
• Student Growth Percentiles are not backed by research on estimating teacher effectiveness. By contrast, research on SGPs has shown them to be poor at isolating teacher influence.
• New Jersey’s Student Growth Percentile measures, at the school level, are significantly statistically biased with respect to student population characteristics and average performance level.

Understanding Student Growth Measures

Two broad categories of methods and models have emerged in state policy regarding development and application of measures of student achievement growth to be used in newly adopted teacher evaluation systems. The first general category of methods is known as value-added models (VAMs) and the second as student growth percentiles (SGPs or MGPs, for “median growth percentile”). Several large urban school districts including New York City and Washington, DC have adopted value-added models and numerous states have adopted student growth percentiles for use in accountability systems. Among researchers it is well understood that these are substantively different measures by design, one being a possible component of the other. But these measures and their potential uses have been conflated by policymakers wishing to expedite implementation of new teacher evaluation policies and pilot programs.[4]

Arguably, one reason for the increasing popularity of the SGP approach across states is the extent of highly publicized scrutiny and large and growing body of empirical research over problems with using VAMs for determining teacher effectiveness.[5] Yet, there has been far less research on using student growth percentiles for determining teacher effectiveness. The reason for this vacuum is not that student growth percentiles are simply immune to problems of value-added models, but that researchers have until recently chosen not to evaluate their validity for this purpose – estimating teacher effectiveness – because they are not designed to infer teacher effectiveness.

Two recent working papers compare SGP and VAM estimates for teacher and school evaluation and both raise concerns about the face validity and statistical properties of SGPs. Goldhaber and Walch (2012) conclude: “For the purpose of starting conversations about student achievement, SGPs might be a useful tool, but one might wish to use a different methodology for rewarding teacher performance or making high-stakes teacher selection decisions” (p. 30).[6] Ehlert and colleagues (2012) note: “Although SGPs are currently employed for this purpose by several states, we argue that they (a) cannot be used for causal inference (nor were they designed to be used as such) and (b) are the least successful of the three models [Student Growth Percentiles, One-Step VAM & Two-Step VAM] in leveling the playing field across schools” (p. 23).[7]

A value-added estimate uses assessment data in the context of a statistical model (regression analysis), where the objective is to estimate the extent to which a student having a specific teacher or attending a specific school influences that student’s difference in score from the beginning of the year to the end of the year – or period of treatment (in school or with teacher). The most thorough of VAMs, more often used in research than practice, attempt to account for: (a) the student’s prior multi-year gain trajectory, by using several prior year test scores (to isolate the extent that having a certain teacher alters that trajectory), (b) the classroom level mix of student peers, (c) individual student background characteristics, and (d) possibly school level characteristics. The goal is to identify most accurately the share of the student’s or group of students’ value-added that should be attributed to the teacher as opposed to other factors outside of the teachers’ control. Corrections such as using multiple years of prior student scores dramatically reduces the number of teachers who may be assigned ratings. For example, when Briggs and Domingue (2011) estimate alternative models to the LA Times (Los Angeles Unified School District) data using additional prior scores, the number of teachers rated drops from about 8,000 to only 3,300, because estimates can only be determined for teachers in grade 5 and above. [8] As such, these important corrections are rarely included in models used for actual teacher evaluation.

By contrast, a student growth percentile is a descriptive measure of the relative change of a student’s performance compared to that of all students.  That is, the individual scores obtained on these underlying tests are used to construct an index of student growth, where the median student, for example, may serve as a baseline for comparison. Some students have achievement growth on the underlying tests that is greater than the median student, while others have growth from one test to the next that is less. That is, the approach estimates not how much the underlying scores changed, but how much the student moved within the mix of other students taking the same assessments.  It uses a method called quantile regression to estimate the rarity that a child falls in her current position in the distribution, given her past position in the distribution (Briggs & Betebenner, 2009).[9]   Student growth percentile measures may be used to characterize each individual student’s growth, or may be aggregated to the classroom level or school level, and/or across children who started at similar points in the distribution to attempt to characterize the collective growth of groups of students.

Many, if not most value-added models also involve normative rescaling of student achievement data, measuring in relative terms how much individual students or groups of students have moved within the large mix of students. The key difference is that the value-added models include other factors in an attempt to identify the extent to which having a specific teacher contributed to that growth, whereas student growth percentiles are simply a descriptive measure of the growth itself.

SGPs can be hybridized with VAMs, by conditioning the descriptive student growth measure on student demographic characteristics. New York State has adopted such a model. However, the state’s own technical report found “Despite the model conditioning on prior year test scores, schools and teachers with students who had higher prior year test scores, on average, had higher MGPs. Teachers of classes with higher percentages of economically disadvantaged students had lower MGPs(p. 1).[10]

Value-added models while intended to estimate teacher effects on student achievement growth, largely fail to do so in any accurate or precise way, whereas student growth percentiles make no such attempt.[11] Specifically, value-added measures tend to be highly unstable from year to year, and have very wide error ranges when applied to individual teachers, making confident distinctions between “good” and “bad” teachers difficult if not impossible.[12]  Furthermore, while value-added models attempt to isolate that portion of student achievement growth that is caused by having a specific teacher they often fail to do so and it is difficult if not impossible to discern a) how much the estimates have failed and b) in which direction for which teachers. That is, the individual teacher estimates may be biased by factors not fully addressed in the models and researchers have no clear way of knowing how much. We also know that when different tests are used for the same content, teachers receive widely varying ratings, raising additional questions about the validity of the measures.[13]

While we have substantially less information from existing research on student growth percentiles, it stands to reason that since they are based on the same types of testing data, they will be similarly susceptible to error and noise. But more troubling, since student growth percentiles make no attempt (by design) to consider other factors that contribute to student achievement growth, the measures have significant potential for omitted variables bias.  SGPs leave the interpreter of the data to naively infer (by omission) that all growth among students in the classroom of a given teacher must be associated with that teacher. Research on VAMs indicates that even subtle changes to explanatory variables in value-added models change substantively the ratings of individual.[14] Omitting key variables can lead to bias and including them can reduce that bias.  Excluding all potential explanatory variables, as do SGPs, takes this problem to the extreme by simply ignoring the possibility of omitted variables bias while omitting a plethora of widely used explanatory variables. As a result, it may turn out that SGP measures at the teacher level appear more stable from year to year than value-added estimates, but that stability may be entirely a function of teachers serving similar populations of students from year to year. The measures may contain stable omitted variables bias, and thus may be stable in their invalidity. Put bluntly, SGPs may be more consistent by being more consistently wrong.

In defense of Student Growth Percentiles as accountability measures, Betebenner, Wenning and Briggs (2011) explain that one school of thought is that value-added estimates are also most reasonably interpreted as descriptive measures, and should not be used to infer teacher or school effectiveness: “The development of the Student Growth Percentile methodology was guided by Rubin et al’s (2004) admonition that VAM quantities are, at best, descriptive measures”.[15] Rubin, Stuart, and Zanutto (2004) explain:

Value-added assessment is a complex issue, and we appreciate the efforts of Ballou et al. (2004), McCaffrey et al. (2004) and Tekwe et al. (2004). However, we do not think that their analyses are estimating causal quantities, except under extreme and unrealistic assumptions. We argue that models such as these should not be seen as estimating causal effects of teachers or schools, but rather as providing descriptive measures (Rubin et al., 2004, p. 18).[16]

Arguably, these explanations do less to validate the usefulness of Student Growth Percentiles as accountability measures (inferring attribution and/or responsibility to schools and teachers) and far more to invalidate the usefulness of both Student Growth Percentiles and Value-Added Models for these purposes.

Do Growth Percentiles Fully Account for Student Background?

New Jersey has recently released its new regulations for implementing teacher evaluation policies, with heavy reliance on student growth percentile scores, aggregated to the teacher level as median growth percentiles (using the growth percentile of the median student in any class as representing the teacher effect). When recently challenged about whether those growth percentile scores will accurately represent teacher effectiveness, specifically for teachers serving kids from different backgrounds, NJ Commissioner Christopher Cerf explained:

“You are looking at the progress students make and that fully takes into account socio-economic status,” Cerf said. “By focusing on the starting point, it equalizes for things like special education and poverty and so on.”[17] (emphasis added)

There are two issues with this statement. First, comparisons of individual students don’t actually explain what happens when a group of students is aggregated to their teacher and the teacher is assigned the median student’s growth score to represent his/her effectiveness, where teachers don’t all have an evenly distributed mix of kids who started at similar points (to other teachers). So, in one sense, this statement doesn’t even address the issue.

Second, this statement is simply factually incorrect, even regarding the individual student. The statement is not supported by research on estimating teacher effects which largely finds that sufficiently precise student, classroom and school level factors do relate to variations not only in initial performance level but also in performance gains. Those cases where covariates have been found to have only small effects are likely those in which effects are either drowned out by particularly noisy outcome measures, problems resulting from underlying test scaling (or re-scaling) or poorly measured student characteristics. Re-analysis of teacher ratings from the Los Angeles Times analysis, using richer data and more complex value-added models yielded substantive changes to teacher ratings.[18] The Los Angeles Times model already included far more attempts to capture student characteristics than New Jersey’s Growth Percentile Model – which includes none.

At a practical level, it is relatively easy to understand how and why student background characteristics affect not only their initial performance level but also their achievement growth. Consider that one year’s assessment is given in April. The school year ends in late June. The next year’s test is given the next April. First, there are approximately two months of instruction given by the prior year’s teacher that are assigned to the current year’s teacher. Beyond that, there are a multitude of things that go on outside of the few hours a day where the teacher has contact with a child, that influence any given child’s “gains” over the year, and those things that go on outside of school vary widely by children’s economic status. Further, children with certain life experiences on a continued daily, weekly and monthly basis are more likely to be clustered with each other in schools and classrooms.

With annual test scores, differences in summer experiences which vary by student economic background matter. Lower income students experience much lower achievement gains than their higher income peers over the summer.[19] Even the recent Gates Foundation Measures of Effective Teaching Project, which used fall and spring assessments, found that “students improve their reading comprehension scores as much (or more) between April and October as between October and April in the following grade.”(p. 8)[20] That is, gains and/or losses may be as great during the time period when children have no direct contact with their teachers or schools. Thus, it is rather absurd to assume that teachers can and should be evaluated based on these data.

Even during the school year, differences in home settings and access to home resources matter, and differences in access to outside of school tutoring and other family subsidized supports may matter and depend on family resources. [21] Variations in kids’ daily lives more generally matter (neighborhood violence, etc.) and many of those variations exist as a function of socio-economic status. Variations in peer group with whom children attend school matters,[22] and also varies by socio-economic status, neighborhood structure, conditions, and varies by socioeconomic status of not just the individual child, but the group of children.

In short, it is inaccurate to suggest that using the same starting point “fully takes into account socio-economic status.” It’s certainly false to make such a statement about aggregated group comparisons – especially while never actually conducting or producing publicly any analysis to back such a claim.

Did the Gates Foundation Measures of Effective Teaching Study Validate Use of Growth Percentiles?

Another claim used in defense of New Jersey’s growth percentile measures is that a series of studies conducted with funding from the Bill and Melinda Gates Foundation provide validation that these measures are indeed useful for evaluating teachers. In a recent article by New Jersey journalist John Mooney in his online publication NJ Spotlight, state officials were asked to respond to some of the above challenges regarding growth percentile measures. Along with perpetuating the claim that the growth percentile model takes fully into account student background, state officials also issued the following response:

“The Christie administration cites its own research to back up its plans, the most favored being the recent Measures of Effective Teaching (MET) project funded by the Gates Foundation, which tracked 3,000 teachers over three years and found that student achievement measures in general are a critical component in determining a teacher’s effectiveness.”[23]

The Gates Foundation MET project did not study the use of Student Growth Percentile Models. Rather, the Gates Foundation MET project studied the use of value-added models, applying those models under the direction of leading researchers in the field, testing their effects on fall to spring gains, and on alternative forms of assessments. Even with these more thoroughly vetted value-added models, the Gates MET project uncovered, though largely ignored, numerous serious concerns regarding the use of value-added metrics. External reviewers of the Gates MET project reports pointed out that while the MET researchers maintained their support for the method, the actual findings of their report cast serious doubt on its usefulness.[24]

The Gates Foundation MET project results provide no basis for arguing that student growth percentile measures should have a substantial place in teacher evaluation.  The Gates MET project never addressed student growth percentiles. Rather, it attempted a more thorough, more appropriate method, but provided results which cast serious doubt on the usefulness of even that method.  Those who have compared the relative usefulness of growth percentiles and value-added metrics have found growth percentiles sorely lacking as a method for sorting out teacher influence on student gains.[25]

What do We Know about New Jersey’s Growth Percentile Measures?

Unfortunately, the New Jersey Department of Education has a) not released any detailed teacher-level growth percentile data for external evaluation or review, b) unlike other states pursuing value-added and/or growth metrics has chosen not to convene a technical review panel and c) unlike other states pursuing these methods, has chosen not to produce any detailed technical documentation or analysis of their growth percentile data. Yet, they have chosen to issue regulations regarding how these data must be used directly in consequential employment decisions. This is unacceptable.

The state has released as part of its school report cards, school aggregate median growth percentile data, which shed some light on the possible extent of the problems with their current measures.  A relatively straightforward statistical check on the distributional characteristics of these measures is to evaluate the extent to which they relate to measures of student population characteristics. That is, to what extent do we see that higher poverty schools have lower growth percentiles, or to what extent do we see that schools with higher average performing peer groups have higher average growth percentiles. Evidence of correlation with either might be indicative of statistical bias- specifically omitted variables bias.

Table 1 below uses school level data from the recently released New Jersey School Report Cards databases, combined with student demographic data from the New Jersey Fall Enrollment Reports.  For both ELA and Math growth percentile measures, there exist modest, negative statistically significant correlations with school level % free lunch, and with school level % black or Hispanic.

Higher shares of low income children and higher shares of minority children are each associated with lower average growth percentiles.  This finding validates that the growth percentile measures – which fail on their face to take into account student background characteristics – as a result fail statistically to remove the bias associated with these measures.

To simplify, there exist three types of variation in the growth percentile measures: 1) variation that may in fact be associated with a given teacher or school, 2) variation that may be associated with factors other than the school or teacher (omitted variables bias) and 3) statistical/measurement noise.

The difficulty here is our inability to determine which type of variation is “true effect”, which is the “effect of some other factor” and which is “random noise.” Here, we can see that a sizeable share of the variance in growth is associated with school demographics (“Some other factor”). One might assert that this pattern occurs simply because good teachers sort into schools with fewer low income and minority children, who are then left with bad teachers unable to produce gains. Such an assertion cannot be supported with these data, given the equal (if not greater) likelihood that these patterns occur as a function of omitted variables bias – where all possible variables have actually been omitted (proxied only with a single prior score).

Pursuing a policy of dismissing or detenuring at a higher rate, teachers in high poverty schools because of their lower growth percentiles, would be misguided. Doing so would create more instability and disruption in settings already disadvantaged, and may significantly reduce the likelihood that these schools could then recruit “better” teachers as replacements.

Table 1

	% Free Lunch	% Black or Hispanic
% Black or Hispanic	0.9098*
Math MGP	-0.3703*	-0.3702*
ELA MGP	-0.4828*	-0.4573*

*p<.05

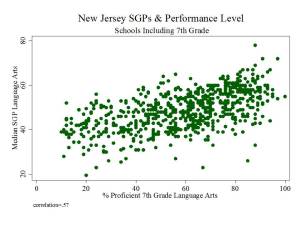
Figure 1 shows the clarity of the pattern of relationship between school average proficiency rates (for 7^th graders) and growth percentiles. Here, we see that schools with higher average performance also have significantly higher growth percentiles. This may occur for a variety of reasons. First, it may just be that along higher regions of the underlying test scale, higher gains are more easily attainable. Second, it may be that peer group average initial performance plays a significant role in influencing gains. Third, it may be that to some extent, higher performing schools do have some higher value-added teachers.

The available data do not permit us to fully distinguish which of these three factors most drives this pattern, and the first two of these factors have little or nothing to do with teacher or teaching quality. This uncertainty raises issues of fairness and reliability; particularly, in an evaluation system that has implications for teacher tenure and other employment.

Figure 1

Figure 2 elaborates on the negative relationship between student low income status and school level growth percentiles, showing that among very high poverty schools, growth percentiles tend to be particularly low.

Figure 2

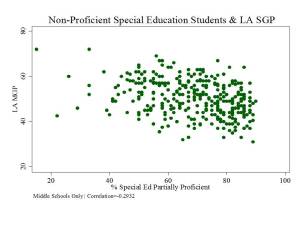
Figure 3 shows that the share of special education children scoring non-(partially)-proficient also seems to be a drag on school level growth percentiles. Schools with larger shares of partially proficient special education students tend to have lower median growth percentiles.

Figure 3

An important note here is that these are school level aggregations and much of the intent of state policy is to apply these growth percentiles for evaluating teachers. School growth percentiles are merely aggregations of the handful of teachers for whom rating exist in any school. Bias that appears at the school level is not created by the aggregation. It may be clarified by the aggregation. But if the school level data are biased, then so too are the underlying teacher level data.

What Incentives and Consequences Result from these Measures?

The consequences of adopting these measures for high stakes use in policy and practice are significant.

Rating Schools for Intervention

Growth measures are generally assumed to be better indicators of school performance and less influenced by student background than status measures. Status measures include proficiency rates commonly adopted for compliance with the Federal No Child Left Behind Act.  Using status measures disparately penalizes high poverty, high minority concentration schools, increasing the likelihood that these schools face sanctions including disruptive interventions such as closure or reconstitution. While less biased than status measures, New Jersey’s Student Growth Percentile measures appear to retain substantial bias with respect to student population characteristics and with respect to average performance levels, calling into question their usefulness for characterizing school (and by extension school leader) effectiveness. Further, the measures simply aren’t designed for making such assertions.

Further, if these measures are employed to impose disruptive interventions on high poverty, minority concentration schools, this use will exacerbate the existing disincentive for teachers or principals to seek employment in these schools. If the growth percentiles systematically disadvantage schools with more low income children and non-proficient special education children, relying on these measures will also reinforce current incentives for high performing charter schools to avoid low income children and children with disabilities.

Employment Decisions

First and foremost, SGPs are not designed for inferring the teacher’s effect on student test score change and as such they should not be used that way. It simply does not comport with fairness to continue to use SGPs for an end for which they were not designed. Second, New Jersey’s SGPs retain substantial bias at the school level, indicating that they are likely a very poor indicator of teacher influence. The SGP creates a risk that a teacher will be erroneously deprived of a property right in tenure, consequently creating due process problems. In essence, these two concerns about SGP raise serious issues of validity and reliability. Continued reliance on an invalid/unreliable model borders on arbitrariness.

These biases create substantial disincentives for teachers and/or principals to seek employment in settings with a) low average performing students, b) low income students and c) high shares of non-proficient special education students. Creating such a disincentive is more likely to exacerbate disparities in teacher quality across settings than to improve it.

Teacher Preparation Institutions

While to date, the New Jersey Department of Education has made no specific movement toward rating of teacher preparation institutions using the aggregate growth percentiles of recent graduates in the field, such a movement seems likely. The new Council for the Accreditation of Teacher Preparation standards requires that teacher preparation institutions employ their state metrics for evaluative purposes:

4.1.The provider documents, using value-added measures where available, other state-supported P-12 impact measures, and any other measures constructed by the provider, that program completers contribute to an expected level of P-12 student growth.[26]

The patterns of bias in SGPs being relatively clear, it would be disadvantageous for colleges of education to place their graduates in high poverty, low average performing schools, or schools with higher percentages of non-proficient special education students.

The Path Forward

Given what we know about the original purpose and design of student growth percentiles and what we have learned specifically about the characteristics of New Jersey’s Growth Percentile measures, we propose the following:

(i) An immediate moratorium on attaching any consequences – job action, tenure action or compensation to these measures. Given the available information, failing to do so would be reckless and irresponsible and further, is likely to lead to exorbitant legal expenses incurred by local public school districts obligated to defend the indefensible.

(ii) A general rethinking – back to square one – on how to estimate school and teacher effect, with particular emphasis on better models from the field. It may or may not, in the end, be a worthwhile endeavor to attempt to estimate teacher and principal effects using student assessment data. At the very least, the statistical strategy for doing so, along with the assessments underlying these estimates, require serious rethinking.

(iii) A general rethinking/overhaul of how data may be used to inform thoughtful administrative decision making, rather than dictate decisions.  Data including statistical estimates of school, program, intervention or teacher effects can be useful for guiding decision making in schools. But rigid decision frameworks, mandates and specific cut scores violate the most basic attributes of statistical measures. They apply certainty to that which is uncertain. At best, statistical estimates of effects on student outcomes may be used as preliminary information – a noisy pre-screening tool – for guiding subsequent, more in-depth exploration and evaluation.

Perhaps most importantly, NJDOE must reposition itself as an entity providing thoughtful, rigorous technical support for assisting local public school districts in making informed decisions regarding programs and services.  Mandating decision frameworks absent sound research support is unfair and sends the wrong message to educators who are in the daily trenches At best, the state’s failure to understand the disconnect between existing research and  current practices suggests  a need for critical  technical capacity. At worst, endorsing policy positions through a campaign of disinformation raises serious concerns.

---

[1] http://www.njspotlight.com/assets/13/0401/2229

[2] http://www.njspotlight.com/assets/13/0401/2229

[3] http://www.njspotlight.com/assets/13/0401/2229

[4] Goldhaber, D., & Walch, J. (2012). Does the model matter? Exploring the relationship between different student achievement-based teacher assessments. University of Washington at Bothell, Center for Education Data & Research. CEDR Working Paper 2012-6. Ehlert, M., Koedel, C., &Parsons, E., & Podgursky, M. (2012).  Selecting growth measures for school and teacher evaluations. National Center for Analysis of Longitudinal Data in Education Research (CALDAR). Working Paper #80.

[5] Baker, E.L., Barton, P.E., Darling-Hammond, L., Haertel, E., Ladd, H.F., Linn, R.L., Ravitch, D., Rothstein, R., Shavelson, R.J., & Shepard, L.A. (2010). Problems with the use of student test scores to evaluate teachers. Washington, DC: Economic Policy Institute.  Retrieved June 4, 2012, from http://epi.3cdn.net/724cd9a1eb91c40ff0_hwm6iij90.pdf. Corcoran, S.P. (2010). Can teachers be evaluated by their students’ test scores? Should they be? The use of value added measures of teacher effectiveness in policy and practice. Annenberg Institute for School Reform. Retrieved June 4, 2012, from http://annenberginstitute.org/pdf/valueaddedreport.pdf.

[6] Goldhaber, D., & Walch, J. (2012). Does the model matter? Exploring the relationship between different student achievement-based teacher assessments. University of Washington at Bothell, Center for Education Data & Research. CEDR Working Paper 2012-6.

[7] Ehlert, M., Koedel, C., &Parsons, E., & Podgursky, M. (2012).  Selecting growth measures for school and teacher evaluations. National Center for Analysis of Longitudinal Data in Education Research (CALDAR). Working Paper #80.

[8] See Briggs & Domingue’s (2011) re-analysis of LA Times estimates pages 10 to 12. Briggs, D. & Domingue, B. (2011). Due diligence and the evaluation of teachers: A review of the value-added analysis underlying the effectiveness rankings of Los Angeles Unified School District Teachers by the Los Angeles Times. Boulder, CO: National Education Policy Center. Retrieved June 4, 2012 from http://nepc.colorado.edu/publication/due-diligence.

[9] Briggs, D. & Betebenner, D., (2009, April). Is student achievement scale dependent? Paper presented at the invited symposium Measuring and Evaluating Changes in Student Achievement: A Conversation about Technical and Conceptual Issues at the Annual Meeting of the National Council for Measurement in Education, San Diego, CA. Retrieved June 4, 2012, from http://dirwww.colorado.edu/education/faculty/derekbriggs/Docs/Briggs_Weeks_Is%20Growth%20in%20Student%20Achievement%20Scale%20Dependent.pdf.

[10] American Institutes for Research. (2012). 2011-12 growth model for educator evaluation technical report: Final. November, 2012. New York State Education Department.

[11] Briggs and Betebenner (2009) explain: “However, there is an important philosophical difference between the two modeling approaches in that Betebenner (2008) has focused upon the use of SGPs as a descriptive tool to characterize growth at the student-level, while the LM (layered model) is typically the engine behind the teacher or school effects that get produced for inferential purposes in the EVAAS” (p. 30).

[12] McCaffrey, D.F., Sass, T.R., Lockwood, J.R., & Mihaly, K. (2009). The intertemporal variability of teacher effect estimates. Education Finance and Policy, 4,(4) 572-606. Sass, T.R. (2008). The stability of value-added measures of teacher quality and implications for teacher compensation policy. Retrieved June 4, 2012, from http://www.urban.org/UploadedPDF/1001266_stabilityofvalue.pdf. Schochet, P.Z. & Chiang, H.S. (2010). Error rates in measuring teacher and school performance based on student test score gains. Institute for Education Sciences, U.S. Department of Education. Retrieved May 14, 2012, from http://ies.ed.gov/ncee/pubs/20104004/pdf/20104004.pdf.

[13] Corcoran, S.P., Jennings, J.L., & Beveridge, A.A. (2010). Teacher effectiveness on high- and low-stakes tests. Paper presented at the Institute for Research on Poverty Summer Workshop, Madison, WI.

Gates Foundation (2010). Learning about teaching: Initial findings from the measures of effective teaching project. MET Project Research Paper. Seattle, Washington: Bill & Melinda Gates Foundation. Retrieved December 16, 2010, from http://www.metproject.org/downloads/Preliminary_Findings-Research_Paper.pdf.

[14] Ballou, D., Mokher, C.G., & Cavaluzzo, L. (2012, March). Using value-added assessment for personnel decisions: How omitted variables and model specification influence teachers’ outcomes. Paper presented at the Annual Meeting of the Association for Education Finance and Policy. Boston, MA.  Retrieved June 4, 2012, from http://aefpweb.org/sites/default/files/webform/AEFP-Using%20VAM%20for%20personnel%20decisions_02-29-12.docx.

Briggs, D. & Domingue, B. (2011). Due diligence and the evaluation of teachers: A review of the value-added analysis underlying the effectiveness rankings of Los Angeles Unified School District Teachers by the Los Angeles Times. Boulder, CO: National Education Policy Center. Retrieved June 4, 2012 from http://nepc.colorado.edu/publication/due-diligence.

[15] Betebenner, D., Wenning, R.J., & Briggs, D.C. (2011). Student growth percentiles and shoe leather. Retrieved June 5, 2012, from http://www.ednewscolorado.org/2011/09/13/24400-student-growth-percentiles-and-shoe-leather.

[16] Rubin, D. B., Stuart, E. A., & Zanutto, E. L. (2004). A potential outcomes view of value-added assessment in education. Journal of Educational and Behavioral Statistics, 29(1), 103–16.

[17]http://www.wnyc.org/articles/new-jersey-news/2013/mar/18/everything-you-need-know-about-students-baked-their-test-scores-new-jersy-education-officials-say/

[18] Briggs, D. & Domingue, B. (2011). Due Diligence and the Evaluation of Teachers: A review of the value-added analysis underlying the effectiveness rankings of Los Angeles Unified School District teachers by the Los Angeles Times. Boulder, CO: National Education Policy Center. Retrieved [date] from http://nepc.colorado.edu/publication/due-diligence.

[19] Alexander, K. L., Entwisle, D. R., & Olson, L. S. (2001). Schools, achievement, and inequality: A seasonal perspective. Educational Evaluation and Policy Analysis, 23(2), 171-191.

[20] Learning about Teaching: Initial Findings from the Measures of Effective Teaching Project. MET Project Research Paper. Seattle, Washington: Bill & Melinda Gates Foundation. Retrieved December 16, 2010, from http://www.metproject.org/downloads/Preliminary_Findings-Research_Paper.pdf.

[21] Lubienski, S. T., & Crane, C. C. (2010) Beyond free lunch: Which family background measures matter? Education Policy Analysis Archives, 18(11). Retrieved [date], from http://epaa.asu.edu/ojs/article/view/756

[22] For example, even value-added proponent Eric Hanushek finds in unrelated research that “students throughout the school test score distribution appear to benefit from higher achieving schoolmates.” See: Hanushek, E. A., Kain, J. F., Markman, J. M., & Rivkin, S. G. (2003). Does peer ability affect student achievement?. Journal of applied econometrics, 18(5), 527-544.

[23]http://www.njspotlight.com/stories/13/03/18/fine-print-overview-of-measures-for-tracking-growth/

[24] Rothstein, J. (2011). Review of “Learning About Teaching: Initial Findings from the Measures of Effective Teaching Project.” Boulder, CO: National Education Policy Center. Retrieved [date] from http://nepc.colorado.edu/thinktank/review-learning-about-teaching. [accessed 2-may-13]

[25] Ehlert, M., Koedel, C., Parsons, E., & Podgursky, M. (2012). Selecting Growth Measures for School and Teacher Evaluations. http://ideas.repec.org/p/umc/wpaper/1210.html

[26] http://caepnet.org/commission/standards/standard4/